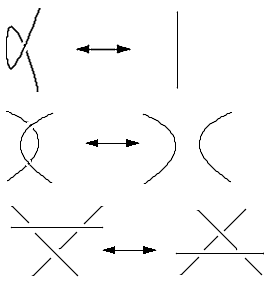How to Draw Celtic Knots

Knot theory developed hugely at the end of the 1980s; the Kaufmann and Jones polynomials were discussed widely in the media and initiated a productive period in mathematics. We have the honor to count amongst the faculty at Strasbourg University one of the leaders in knot theory, Vladimir Turaev, and I had the pleasure of attending a course given by him jointly with Christian Kassel in 1993.

What I want to discuss in this Tutorial, although based on the theory of knots and interlacing, goes back much earlier than this theory, to the Celtic world that was putting knots onto their menhirs in the 4th century BC. By the 6th century, the monks of Ireland who were making many copies of the Bible, Christianized these motifs and incorporated them into the texts of their illuminated manuscripts. The tortured and clever motifs of Saxon helmets and Celtic brooches gave way to big borders, severe and dense. The best examples of these works are found in works such as the Book of Kells (7th century), the Book of Durrow or the Lindisfarne Gospels. It was in the magnificent library of Trinity College Dublin that I had the pleasure of contemplating the first two of these.

To ordinary eyes the designs are just very complicated and very beautiful, but to an initiate such as myself in addition to their splendor as designs I could see a beauty of a different order and the underlying basis of their organization. I fell under the charms of these motifs and decided to chase up the literature on them, design original motifs and create jewelry and other objects based on this technique. Sufficiently keen to share my passion, I gave two series of courses in illumination techniques in the calligraphy school at St Cyr sur Loire in 1994 and 1996.

I thank Richard Forestier, Chantale Facchinetti and Forestier for having the grace and patience to welcome me. Without their care and interest in the subject and their passion for things well made, I would never have prepared this Tutorial and it was thanks to them that I worked out ways to describe intelligibly the mathematical objects (very simple for a mathematician) that form the basis of the theory. I thank them here. My artistic interest has also served as the basis for a theoretical study and my mathematical thesis is based on these techniques which, if not new to mathematics, seem to me to be under-exploited. I hope that this Tutorial will initiate you into these techniques and, in any case, communicate my pleasure in designing these captivating motifs.

A Little Theory

Machine

A knot is what you create when you tangle up a piece of string and join up the two ends, which you can then deform at leisure - that is to say an imbedding of a circle into space. An interlacing is what you get when you let several people play this game within a tight space. A knot is thus an interlacing with one component. If you want to represent an interlacing, you spread the strings onto the ground and only allow the crossing of two strings (no more). Then you draw it by noting carefully which string is 'over' and which 'under' at each crossing. That is to say you produce a 'regular projection on a plane' of the interlacing. The design is a tetravalent planar graph where, on each vertex of the graph you record the 'overs' and 'unders'. You can enrich the structure in all sorts of ways: space out the design a little; make the string 'elastic'; position each knot; leave some knots open with their ends fixed (you're now talking about 'entanglements'); attach a label or a color to each knot or each crossing …

Reidemeister Movements

There are many regular projections of the same interlacing but you can always pass from one to the other with a series of movements which are both sufficient and necessary - Reidemeister movements.

However, it is difficult in practice to determine if two projections belong to the same interlacing.

Graphs

When you consider one part of a design, i.e. a related regular projection, it splits the plane into various zones, the crossings, the edges connecting the vertices (except for the simple circle, i.e. a trivial knot) and zones resembling disks, cells of dimension two. There's one zone that does not resemble a disk - the big zone that extends to infinity. Let's color this zone in black. Now let's decide at each vertex on the edge of a black cell to extend the color black to the opposite cell and so forth.

You then get a partition into black and white zones:

The cells of dimension two thus partition themselves into black and white and it is easy to see that it makes a checkerboard where each crossing has the following appearance:

You code this partitioning into a planar graph with signed edges, assigning a vertex to each white cell and drawing an edge between two cells above each crossing which comes between them.

You then put a sign onto this edge depending on the over-under situation: a + sign if the strand which passes over comes from the left when you place it in a white cell, a - sign otherwise. You can represent the sign of an edge graphically with a solid line if + and a dashed line if -.

This data perfectly encodes the regular projection of the interlacing and there is a mapping between the plane projection of the interlacing and this planar graph with signed edges. On the other hand if you place yourself in a three-dimensional sphere (you add a point at infinity to our usual space) and you project onto the sphere (the 'true' two-dimensional cell), the correspondence is not one-to-one. Two planar graphs with signed edges code for the same projection. Which is the second? It's the dual graph that you get by placing the vertices not at the center of the white cells but of the black cells. They are dual in the sense that ideas of dimension k are replaced by notions of dimension 2-k:

At each edge of one corresponds an edge of the other which cuts it at one single point and its sign is opposite, at each vertex of the one corresponds a face of the other and vice versa. The situation is more symmetrical in the case of the plane, the zone containing the infinity no longer exists and no zone is distinguished from the others, the duality appears.

Reidemeister Moves

The Reidemeister movements translate themselves into graphs by these equivalences:

You go from a line to that below by taking the dual graph [I don't understand]. The little feathers on the vertices show that you only consider one part of the graph, that other edges may connect to these vertices and won't be affected by the moves. It is understood that you must consider the same relations when you invert the signs of all the edges. Each Reidemeister move therefore creates four relations on the graphs. There's a one-to-one correspondence between the wk and the classes of planar graphs with signed edges, module the passage to dual graphs and the movements I', II' and III'.

Cosmetics

If you started with a beautiful graph, all clean, you'll normally end up with a hesitant and dirty design, full of crossings-out, badly rubbed-out lines, lines all the same color, far from the following design:

One tip is to use different pencil leads for the trace of the graph and of the interlacing. First of all make a sketch of the interlacing by slogging through the method rigorously without cheating. Then stand back from it and tidy-up the chaotic path of each thread with a beautiful sinuous curve that takes into account the general direction of the thread. Worry less about the over-under and more about the path of each thread. Having checked each crossing to sort out the over-under, take each thread and consider its knot not like a piece of string, but like a tyre; pump it up and let each bit of tyre take its place. At this point I suggest that you try your hand at a simple border based on a triangular ladder with every 3rd rung missing. Copy the graph on a piece of paper and follow the four steps suggested on the second line:

On the second line I started by applying the method to the letter, with no regard to the aesthetic aspects. That gives corners, hesitant lines and the overs-unders are not yet marked. Then the line is little by little tidied up and its trajectory sorted out. Then the overs-unders are represented and finally the threads are widened. It's obvious that these steps, represented here juxtaposed in reality take place successively in the same place, with much use of the eraser and curses! One of the main problems is that when you rub out a thread, you also rub out the graph beneath. The graph is a guide right to the end and it's an error to think that you can do without it till the picture of the path of the overburdens is clear. It's therefore necessary either to redraw the graph each time you rub out parts of it or, for a preparatory study, to draw on one side of a piece of tracing paper, with the graph on the other side.

The Walls

Compare the preceding braid with that produced from a triangular border from which no edge is missing:

You can see that the omission of an edge changes the results fairly radically. You can also see that to leave out an edge is equivalent to joining two vertices in its dual graph. But if to remove an edge is easy to represent graphically, joining two vertices is less easy. We use the convention that when changing a graph by omitting an edge or, equivalently, by joining two vertices, to draw the graph unchanged but to put a bold line across it if one is erasing the line and to draw the line itself in bold if one identifies its extremities.

By way of example, here is the modified graph associated with the previous triangular braid :

This manner of representation simplifies the graphic representation of the underlying graph but also aids in constructing the interlacing. You just need to consider the bold line, be it longitudinal or transverse, to be a wall on which the knot threads bounce, that is to say a blocked crossing. So there are now four types of "crossing", the +, the - the longitudinal blocks and the transverse blocks. To give a mnemonic: a longitudinal wall closes the door in the middle of the edge, a transverse wall breaks the edge. You can now do most of the exercises in the Annex.

Download The Knotwork Program