Basic Optical Principles for Gemology

The optical characteristics and properties of gemstones often provide the fastest and best methods of identification. A certain amount of theory is necessary as optical principles for gemology determine cutting methods, gemstone attributes and the function of gem testing instruments.

Light

Light and our perception of it play a crucial role in our appreciation of and identification of gemstones. Visible light however comprises only a small part of what is referred to as the electromagnetic spectrum.

While the wave or undulatory theory of light has been mostly superseded by the quantum (particle) theory the wave theory best serves the purpose of describing light for gemmology. We can consider the electromagnetic spectrum to consist of an infinite number of types of wavelengths, from short to very long. Different wavelengths have different powers of penetration dependent upon their length relative to the medium they pass through. X-rays for example with a wavelength near atomic sizes pass through or between most atoms. The amount passed depends upon the mass of the atom concerned.

Dense atoms like lead for instance provide a screen against x-rays. An application of this is a test for diamonds, whether set or unset, where the suspect stones are x-rayed for ten seconds over photographic paper. Carbon atoms are small (low mass) and so diamond is transparent to x-rays and is invisible on the photograph while all diamond simulants show up as positive, opaque shapes.

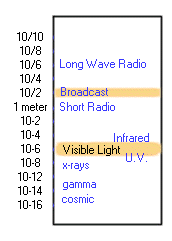
A rough wavelength scale follows:

Note what a small portion of the spectrum comprises visible light. Light can be thought of as progressing outward in a single path (a ray). The ray forms a wave vibrating in all planes at right angles to the direction of travel, the line of the ray.

White light is composed of a mixture of a great many wavelengths each of which is perceived as a different colour. The wavelength of violet light for example is about half that of red light. The wavelengths of white light may be divided into:

• Red 700.0 nm to 640.0 nm
• Orange 640.0 nm to 595.0 nm
• Yellow 595.0 nm to 575.0 nm
• Green 575.0 nm to 500.0 nm
• Blue 500.0 nm to 440.0 nm
• Violet 440.0 nm to 400.0 nm

Transparency Refers to the ease with which light is transmitted through a substance. Classifications of transparency in cut gemstones include:

1. Transparent stones. An object viewed through the gem shows outlines clearly and distinctly (diamond, topaz, corundum).
2. Semi-transparent. Blurred outlines of object but a great deal of light still passes through the stone, i.e. chalcedony.
3. Translucent. Some light passes through, no object can be seen through stone, i.e. opal, some jades, much cryptocrystalline quartz.
4. Semi-translucent. Light is only transmitted through edges, where they are thin, i.e. turquoise.
5. Opaque. No light passes through, i.e. malachite, pyrites.

Colour and degree of colour will affect transparency as will inclusions, flaws, etc. Quality will also affect it. The characteristics are subjective in nature and overlap exists.

Reflection of Light

If a ray of light falls onto a plane mirror the light is reflected away from the surface. The angle of incidence NOI equals the angle of reflection NOR and IO, NO and RO are in the same plane. All angles in optics are measured from the 'normal', an imaginary line at right angles to the surface at the point of incidence (where the light ray strikes the surface).

Refraction

A ray light entering an optically denser medium is bent (refracted) towards the normal. The greater the bending (refraction) for a given angle of incidence the greater is the refractive power of the stone.

The cause of refraction is that the light waves (300,000 km/second) are slowed down as they enter the optically denser medium. In the 17th century Snell (Dutch scientist) described laws relating angles of incidence and refraction for two media. There is a constant ratio between the sines of these angles for any given two media. The constant ratio obtained is called the refractive index. Air is chosen as the rarer medium and yellow sodium light is the standard for refractive index measurements. Refractive index is a measure of a gem's refractive power. It is the ratio of the sine of the angle of incidence divided by the sine of the angle of refraction when light passes from air into the denser medium.

Gems refractive indices range from under 1.5 to over 2.8.

Total Internal Reflection

A ray passing in the opposite direction, from the denser to the rarer (gem to air) medium is bent (refracted) away from the normal.

As the angle of incidence is increased the angle of refraction away from the normal increases until a point is reached when the ray I1OR1 exits parallel to the table of the stone. Any further increase in this angle causes the ray to be totally reflected back into the gem. Ray I2OR2 has been reflected back into the gemstone. This is called total internal reflection and the angle I1OM is called the critical angle for the medium in question. The brilliant cut of diamonds uses total internal reflection and the critical angle for diamond and air to ensure that all light entering the stone is totally reflected and passes out the table or crown facets of the stone. The critical angle is also what enables a refractometer to differentiate gemstones of different species.

Dispersion

A white light ray entering an optically denser medium and leaving by a plane inclined to that of entry will have its colours separated, analyzed, spread out. This is because each colour has a different wavelength and so is differently slowed down (refracted) by the medium. Red (longest wavelength) is slowed the least and violet (shortest wavelength) the most.

This spreading is termed dispersion. In gemstones the effect gives rise to the stone's 'fire'. It may be measured with complex equipment and numerical values given. The higher the number the greater the fire where the stone's colour does not mask the effect, as in demantoid (green) garnet with a greater dispersion (.057) than diamond (.044). With practice and standard stones numerical estimates of dispersion may be made with the Hanneman/Hodgkinson slit technique.

Plane Polarized Light

When a light ray passes through a doubly refractive gemstone it is split into two rays with different amounts of refraction. Each ray is plane polarized, that is instead of the wave vibrating all directions about the line of the ray it vibrates in a single plane only. Each ray is plane polarized at right angles to the other. As each ray is differently refracted so it is differently absorbed by the stone and possesses in coloured gems a different hue or colour.

The Dichroscope picks up each ray at the same time and allows one to view them side by side. A simple dichroscope is a block of calcite with black paper glued to one end which has a small rectangular hole cut in it. The viewer sees two images because the light ray has been split by the high double refraction of calcite. Each image is of a different ray (each ray is also plane polarized at right angles to the other - this is what allows the calcite to present them separately). If a difference in colour exists it will be visible by comparison. One must always test in several directions. This can be of some use in identifying gemstones by their characteristic dichroic or trichroic colours but is usually used as a method of detecting double refraction.

Presence of dichroism proves double refraction. Absence does not mean a material is not doubly refractive - it may be that the dichroism is very weak, or in transparent stones there is none evident. It can be used to find an optic axis. If three colours (trichroic) are seen it means the stone is biaxial. If two only are seen it is uniaxial. Transmitted, not reflected light must be used as reflected light may be partly polarized. Most natural corundum is cut with the table oriented to the optic axis and will show no dichroism through the table. Most synthetic corundum has the table parallel to the optic axis and dichroism is strongest through the table. This is then an indication of synthetic origin.